[BUUCTF]rsa
给了两个文件, 一个加密后的文件, 一个公钥,
开始我以为是用公钥去解密私钥加密的文件,
但是很多加密库都没有提供这样的功能, 比如OpenSSL,
只有用公钥验签的功能.
看了别人的WP才知道这个题是分解公钥的模来实现算出私钥再进行解密.
用OpenSSL可以查看公钥的一些信息
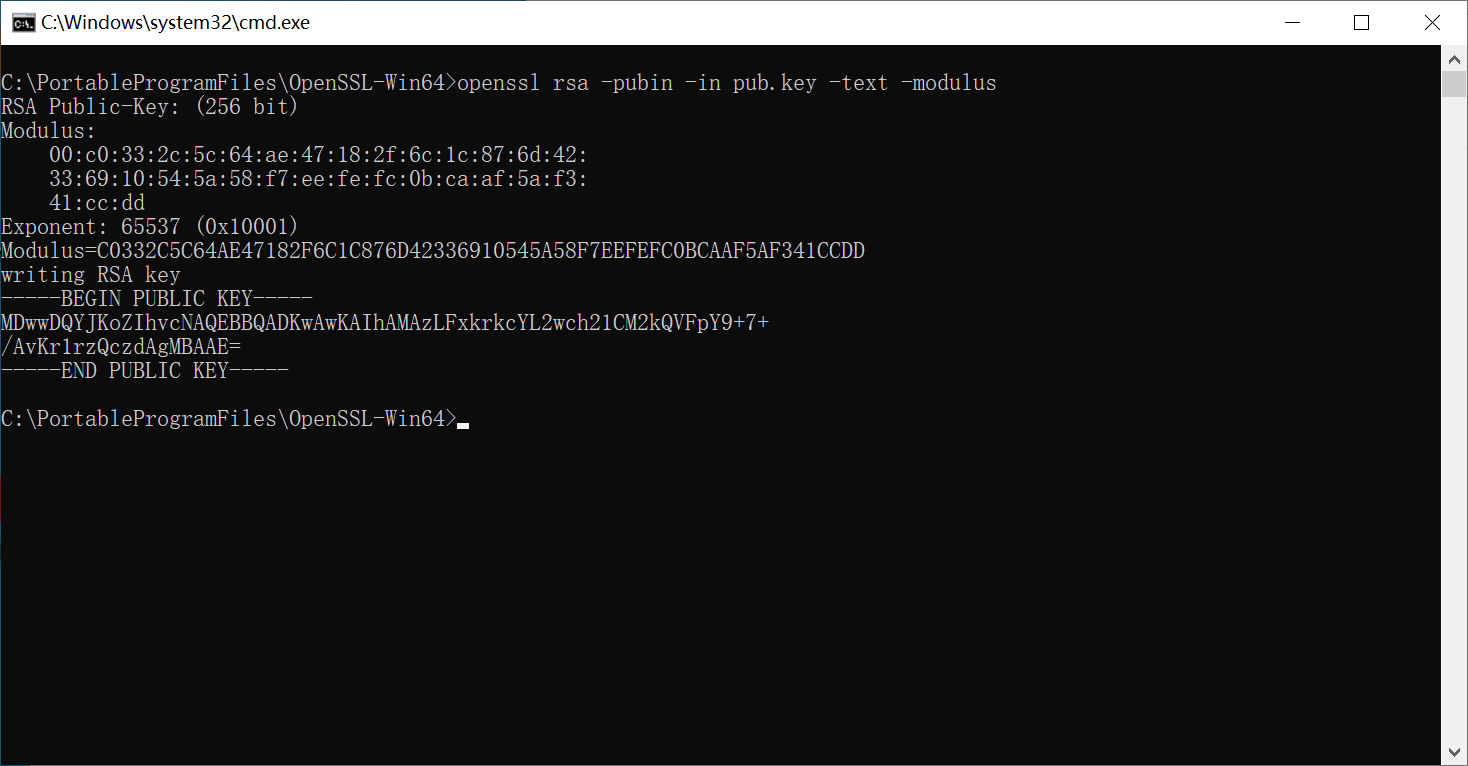
我们可以得知 \[ \begin{aligned} &e=65537\\ &n=C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD \end{aligned} \]
而且公钥比常见的要短很多, 只有256Bit,
这为攻击提供了方便
一些分解模的工具:
RsaCtfTool: Github //这个工具不支持Windows
yafu: Sourceforge
Msieve: Sourceforge
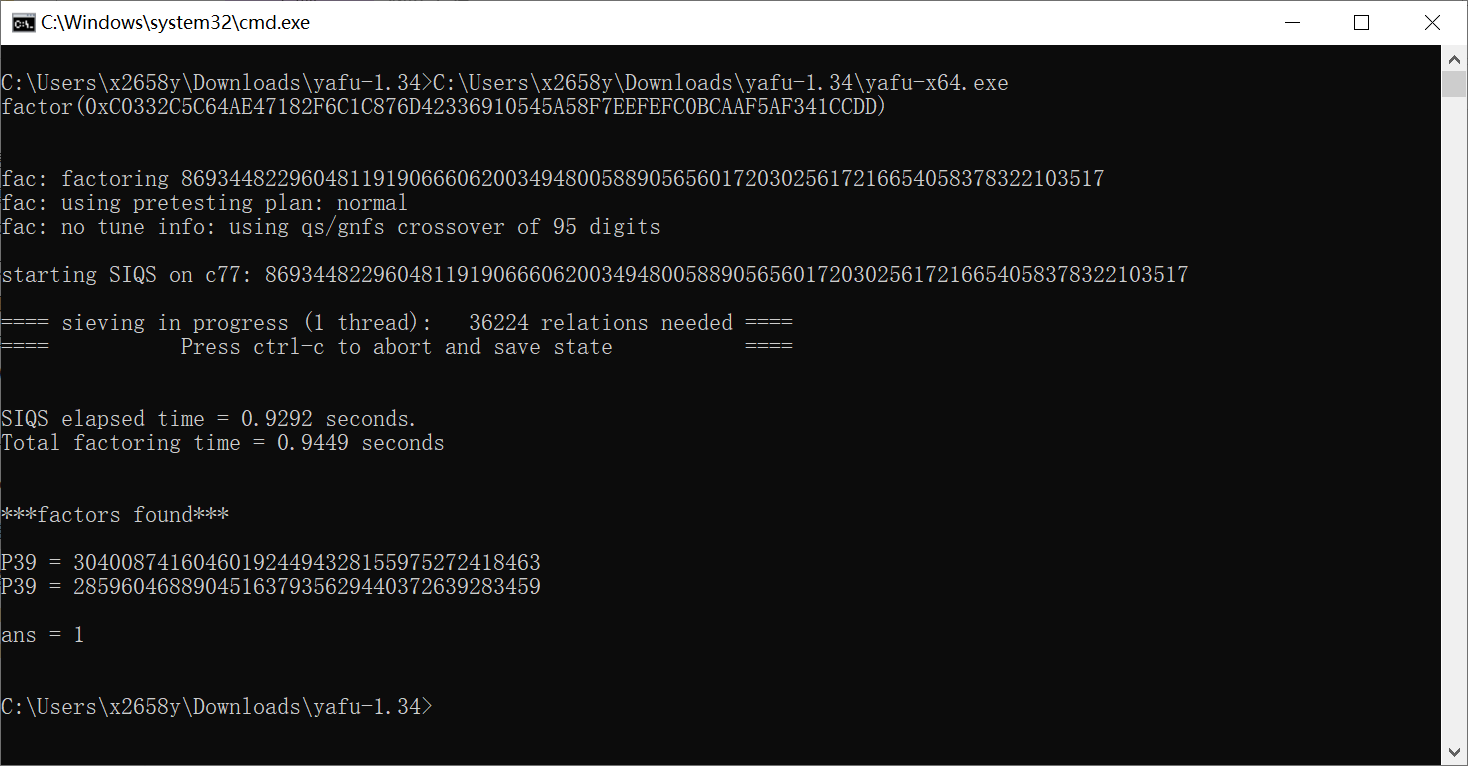
yafu方式, 运行后进入yafu命令行, 输入
1 | factor(0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD) |
即可开始分解
RsaCtfTool方式, 安装好后输入
1 | ./RsaCtfTool.py -n 0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD -e 65537 --private --dumpkey |
工具就会综合判断自动采用合适的方式得出私钥(也可以直接用这个工具解密文件, 详细用法见Github)
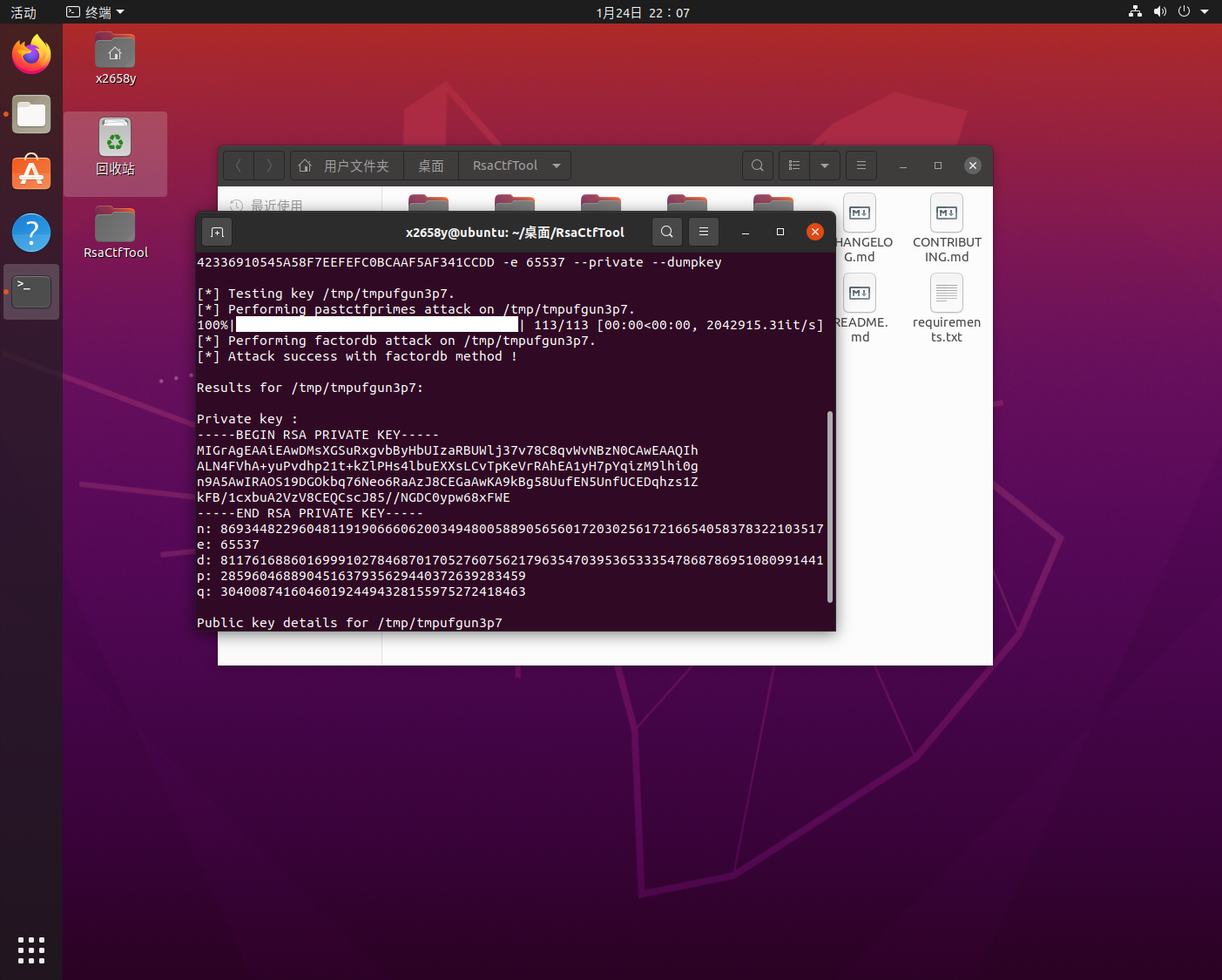
RsaCtfTool已经帮我们生成好了私钥,
如果是用yafu的话还需要计算一下d
我们已经得出 \[ \begin{aligned} &p=285960468890451637935629440372639283459 \\ &q=304008741604601924494328155975272418463 \end{aligned} \]
有了\(p\)和\(q\)就可以轻松求出欧拉函数的值
\[\phi(n)=\phi(p)\times\phi(q)=(p-1)\times(q-1)\]
根据公式 \(ed\equiv1(\mod\phi(n))\),
则d是e模\(\phi(n)\)的模逆元,
Python可以通过gmpy2这个库来求得
1 | from Crypto.PublicKey import RSA |